Predictive Finite Element Models
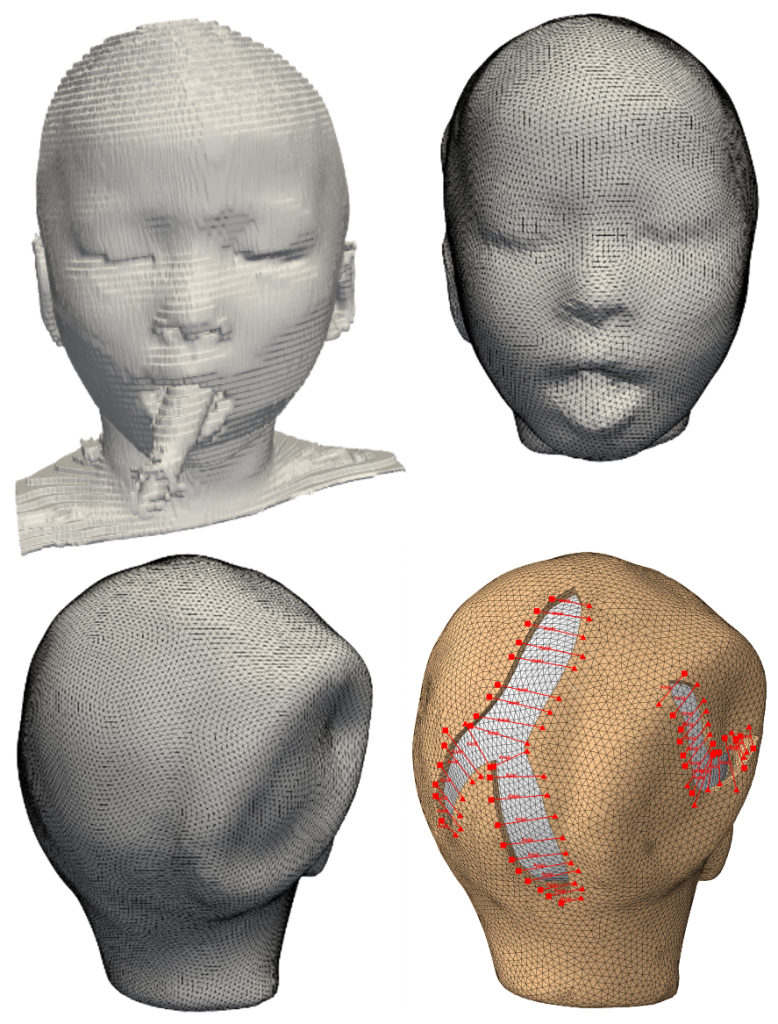
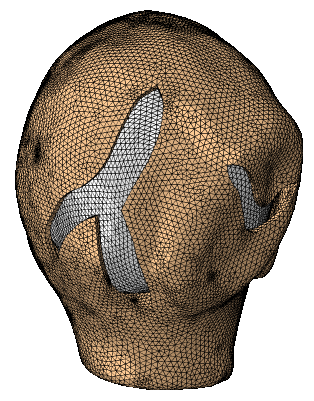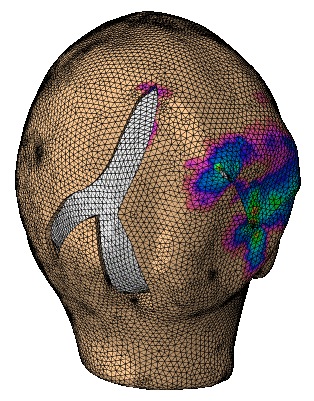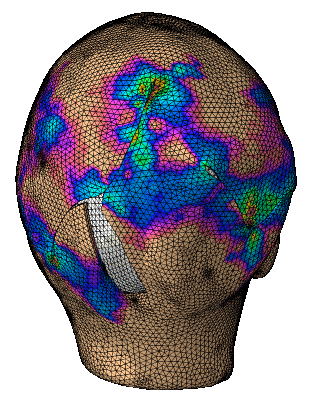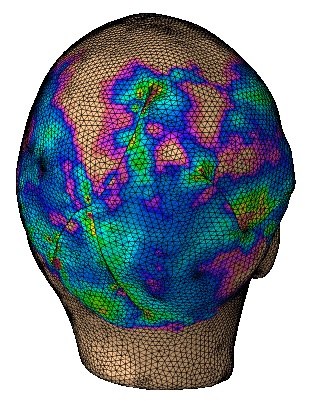
Excessive deformation and stress of skin following reconstructive surgery plays a crucial role in wound healing, often leading to complications. Yet, despite of this concern, surgeries are still planned and executed based on each surgeon’s training and experience rather than quantitative engineering tools. The limitations of current treatment planning and execution stem in part from the difficulty in predicting the mechanical behavior of skin, challenges in directly measuring stress in the operating room, and inability to predict the long term adaptation of skin following reconstructive surgery. Computational modeling of soft tissue mechanics has emerged as an ideal candidate to determine stress contours over sizable skin regions in realistic situations. Virtual surgeries with computational mechanics tools will help surgeons explore different surgeries preoperatively, make prediction of stress contours, and eventually aid the surgeon in planning for optimal wound healing.
Surrogate Modeling for Uncertainty Analysis
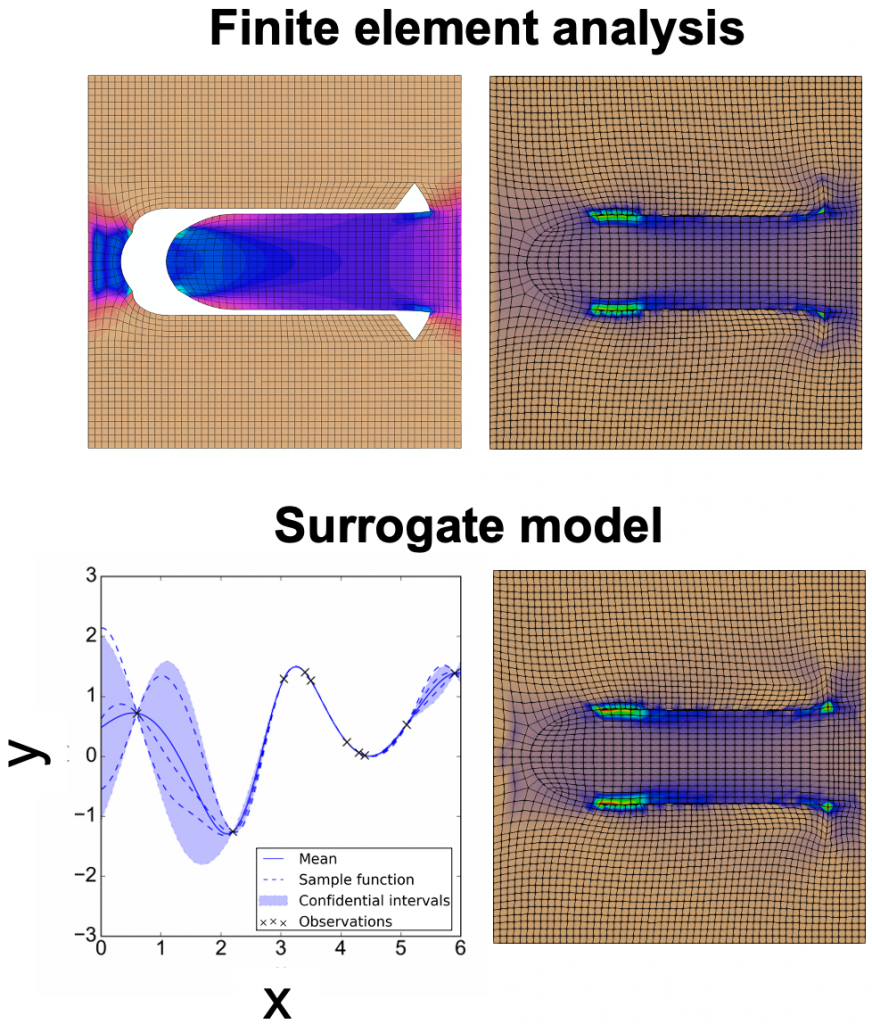
Dealing with the inherent variability of mechanical properties and biological response of biological systems still remains a challenge. Skin properties and adaptation to mechanical cues changes with patient demographic, anatomical location, and from one individual to another. Thus, the precise model parameters can never be known exactly, even if some measurements are available. To handle uncertainty propagation, however, Monte Carlo approach with high fidelity finite element model might not be feasible due to the cost, and therefore the forward function can be substituted for a surrogate model. The probabilistic surrogates enable not only tasks such as fast prediction and uncertainty quantification, but also optimization. In addition to application on soft tissues, the surrogate modeling and method can be further exanded into other engineering fields where uncertainty quantification is needed.
Numerical Characterization of Inelastic Behavior
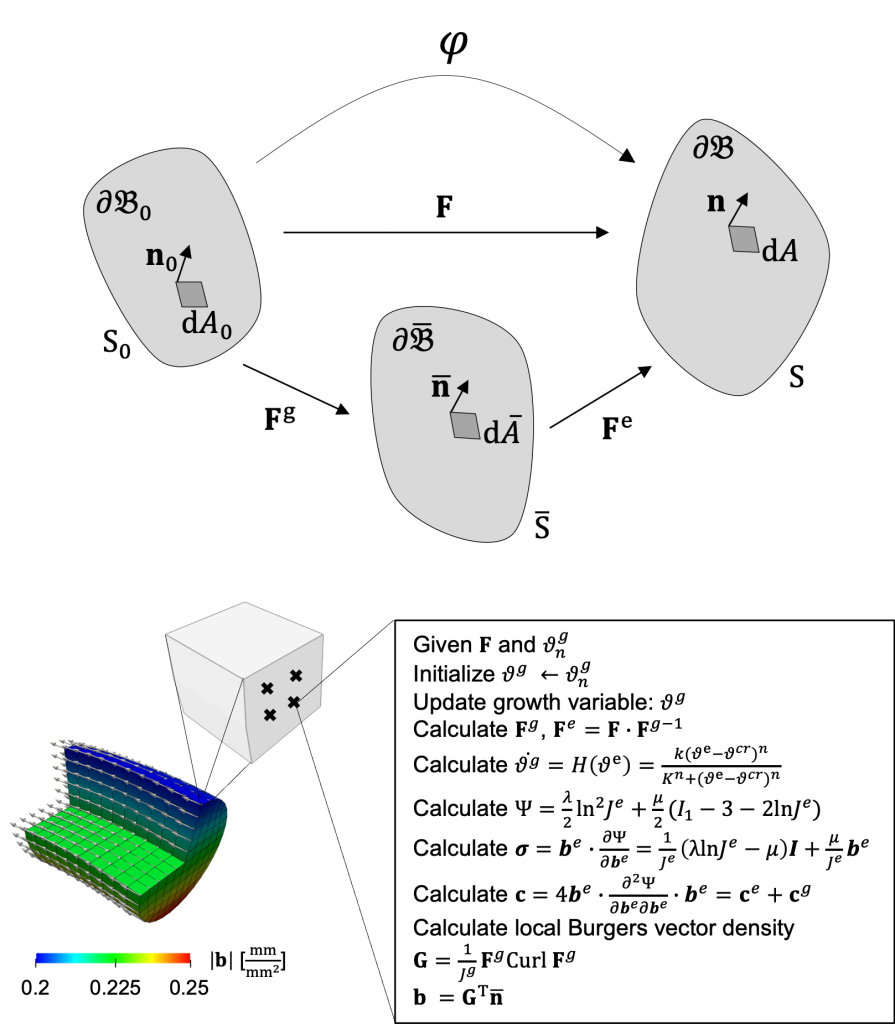
As we grow, our tissues adapt to different physiological and disease conditions through growth and remodeling. This adaptation occurs at the microscopic scale, where cells control the microstructure of their immediate extracellular environment to achieve homeostasis. The local and heterogeneous nature of this process is the source of residual stresses. At the macroscopic scale, growth and remodeling can be accurately captured with the finite volume growth framework within continuum mechanics, which is akin to plasticity. The multiplicative split of the deformation gradient into growth and elastic contributions brings about the notion of incompatibility as a plausible description for the origin of residual stress. Introducing the geometric incompatibility tensor within a finite element framework, we can define the geometric features that characterize incompatibility in biological materials where the constraints and properties associated with growth lead to specific patterns of the incompatibility metrics. Numerical characterization of incompatibility and residual stress can also be applied to biomedical applications.
Life Prediction Method for Engineering Materials
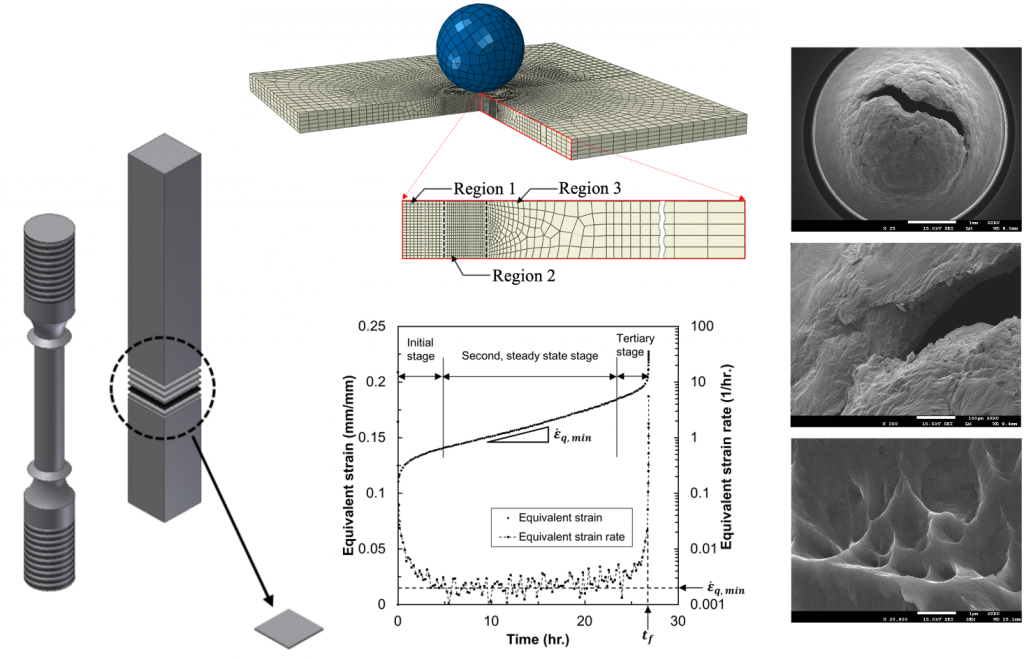
Mechanical characterization of materials is one of fundamental factors for engineering design and structural analysis. Beyond elastic limit, materials show different behavior such as inelastic and nonlinear deformation. Given high temperature, for example, loading even under yield strength can result in time-dependent deformation, so called creep, and finally cause materials failure. Conventional methodologies have been well developed to investigate such materials’ behavior and various studies based on experimental and theoretical approaches are reported. However, classic methods might sometimes have limitation in which the cost is too high or regression method yields overfitting or underfitting. Instead, we focus on data that let speak for themselves and strive to gain insight even into complementary experiment methodology such as Small Punch Creep Test.